Navegación de círculo máximo en la ortodrómica de naranja


Si has estado volando alguna vez desde Londres o Hamburgo a Los Ángeles, te habrás dado cuenta de que nada más despegar, el rumbo es casi hacía noroeste, para llegar finalmente en California con rumbo de sur-oeste. La distancia más corta entre 2 lugares en el mundo no sigue ningún rumbo de brújula fijo al que el capitán podría seguir durante todo el camino. Esto ya sabían los viejos marineros, el rumbo de brújula hay que cambiar continuamente. Esto se llama navegación en el círculo máximo, ya que se viaja en un curso ortodrómica por el mundo.
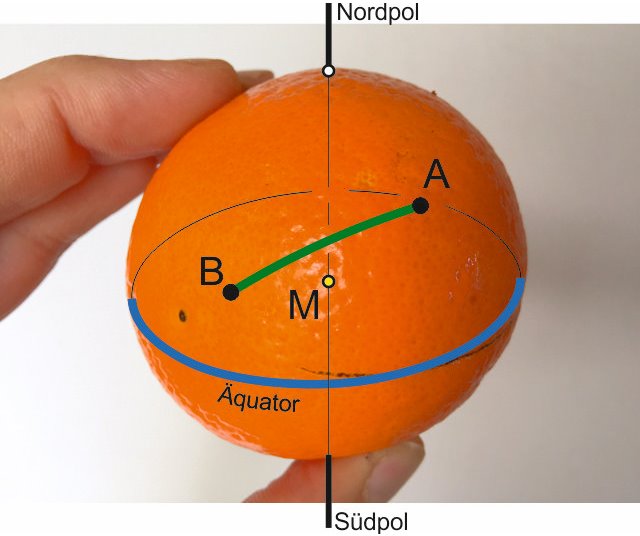
queremos navegar desde A a B, se conocen las coordenadas (longitud y latitud) de la salida y del destino, lo que queremos saber es:
- la distancia
- el rumbo de brújula al que tenemos que seguir
La distancia puede ser calculada por la siguiente relación, tomada de fuentes pertinentes (Wikipedia)


Si aún convertimos el resultado de grados en minutos de arco (multiplicar por 60) obtenemos la distancia entre A y B en millas náuticas (un minuto de arco en un círculo máximo corresponde por definición a una milla náutica).
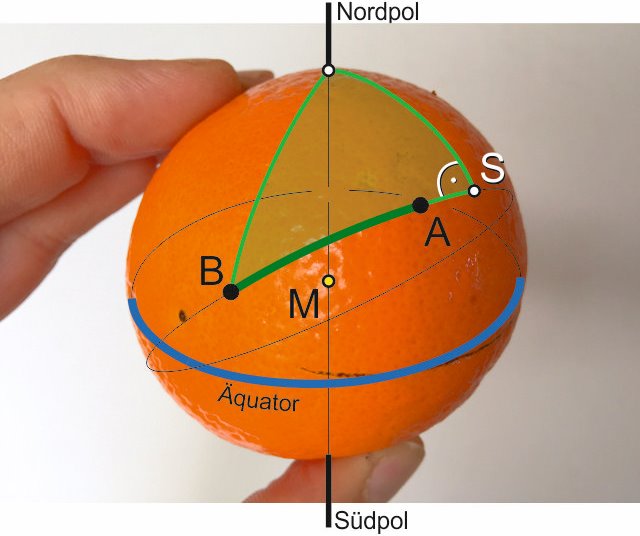
Hasta aquí todo bien. Ahora el rumbo. La navegación clásica propone para esto el método del "triángulo de navegación", que es un triángulo esférico llamado "triángulo de polo" que forma un ángulo recto en el vértice (S) entre el curso de círculo máximo y la distancia al Polo Norte (o al Polo Sur):
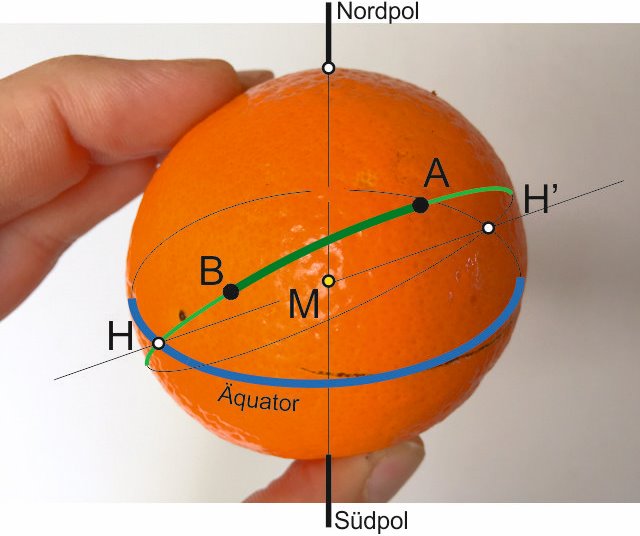
Después de estar un tiempo ocupado con esto, recordé un método más sencillo de entender para mí. Como un viejo pensador intransigente prefiero orientarme relacionado al ecuador en lugar del Polo Norte (tal vez sólo porque hace más calor allí...) Para esto he utilizado el hecho de que cada círculo máximo se cruza exactamente dos veces con cualquier otro del mismo globo, es decir, a los 2 puntos exactamente opuestos de la esfera (llamémoslos H). Así también lo hace el ecuador con nuestro curso de círculo máximo, de la siguiente manera:
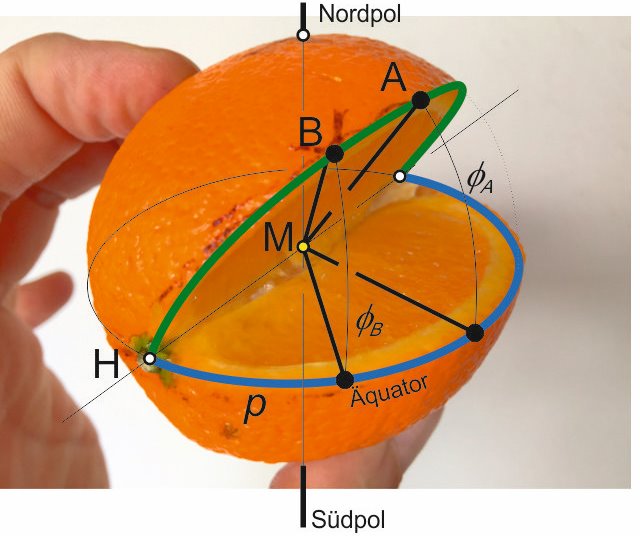
Para que sea un poco más fácil para los ojos humanos, corté nuestra naranja, pues la corté exactamente la parte donde la línea ecuatorial cruza con nuestro curso de círculo máximo, el resultado es el siguiente:
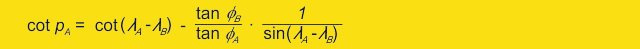
Voy a evitar explicar la derivación de esta ecuación por el momento, las personas interesadas la pueden encontrar más abajo en esta página.
pA nos dice los grados longitudinales que hay que pasar para llegar al bautismo ecuatorial, o hablada como verdulero, el pico de nuestro corte de naranja.
Y con la siguiente ecuación podemos obtener el ángulo en que cortamos la naranja:

(Derivación para los interesados más abajo).
Y ahora, lo que realmente queríamos, una ecuación con la que podemos determinar la latitud correspondiente en el círculo máximo para cualquier longitud dada:

(Derivación como siempre abajo)
Todavía se podía continuar con esto, por ejemplo, sería muy interesante para cada punto de referencia, en qué dirección hay que navegar (el cambio de rumbo de brújula), o determinar la longitud en función de la latitud, o incluso una fórmula para el rumbo sobre tierra, dependiendo de la distancia ya navegada. Con las bases ya desarrolladas se puede derivar todo esto con relativa rapidez con la trigonometría esférica, pero sí que no voy a exagerar aquí...
Lo que nos queda es un
cálculo de prueba:
Acabamos pasar Cabo Horno, y nos gustaría cruzar el Pacífico para llegar a las Islas Fiji. Por supuesto que no haríamos esto normalmente, pero como ejemplo de cálculo funciona agradable :-)
Cabo Horno:
55 grados 59 min S = -55,98 grados
67 grados 17 min W = -67,28 grados
Islas Fiji:
18 grados 8 min S = -18,13 grados
178 grados 26 min O = 178,43 grados
Primero se determina la distáncia para navegar:


= -0,8288 x -0,3112 + 0,5595 x 0,9504 x -0,4114
= -0,0400
arc cos -0,0400 = 87,71 grados (x 60)
= 5.262 millas nauticas
Ahora determinamos el pA requerido:
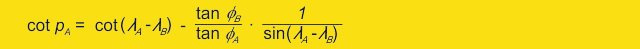
= -0,4513 - 0,2210 x 1,0971
= -0,6938
pA = -55,25 grados
así como el ángulo como cortamos la naranja:

= -0,6750 x -0,8216
= 0,5545
el ángulo de corte de la naranja es entonces 61 grados.
Que pA es negativo significa simplemente, que todavía no hemos llegado al cenit de nuestro círculo máximo durante nuestro viaje, por lo que este valor se refleja a la intersección que tenemos detrás (H' en lugar de H), respectivamente, el ángulo hasta allí.
Ahora queremos determinar cinco puntos en el curso, uno a la salida, otro a la llegada, y tres más en el medio. Nuestra fórmula:

Nuestros longitudes predeterminadas son: -67,28 grados (Cabo Horno, salida); 178,43 grados (Islas Fiji, destino); y también -95 grados; -125 grados; -150 grados. También calculamos el inicio y el destino, aunque ya se conoce las latitudes, sólo para comprobar la exactitud del cálculo.
= 1,8034 x -0,8216 = -1,4817 -> latitud = -55,98 grados, ok para Cabo Horno
= 1,8034 x -0,1815 = -0,3274 -> latitud = -18,13 grados, ok para Islas Fiji
y los 3 puntos de referencia:
= 1,8034 x -0,9925 = -1,7899 -> latitud = -60,81 grados
= 1,8034 x -0,9207 = -1,6604 -> latitud = -58,94 grados
= 1,8034 x -0,6695 = -1,2074 -> latitud = -50,36 grados
Se ve que nuestro curso de círculo máximo nos lleva desde el Cabo Horno inicialmente hacia el sur, hasta 61 grados de latitud (= ángulo de corte de la naranja), probablemente tenemos que luchar duro con hielo allí, antes de que nos dirigimos hacia el norte y se calentará hacia el ecuador...
John Franklin, Amerigo Vespucci y Sir Francis Drake dejan saludar, que no te olvides llevar tu sextante en tu viaje por favor, porque todos eran grandes matemáticos y aún navegando sin GPS...
"Hay algo más importante que la lógica: La imaginación", Alfred Hitchcock
Derivaciones:
Consideramos el triángulo esférico entre el ecuador, nuestro curso de círculo máximo, y un punto arbitrario P (ver imagen 5). Este triángulo tiene excelentes propiedades, es de hecho un triángulo esférico con ángulo recto, y permite por lo tanto fácilmente muchos cálculos. Estamos interesados en la ubicación exacta del corte de la naranja, donde nuestro curso cruza el ecuador, y el ángulo en el que cortamos la naranja. Conocidas son 2 lugares P, es decir, el punto de inicio y del destino, cada uno con latitud y longitud. En este triángulo utilizamos un teorema de la trigonometría esférica:

ahora reemplazamos hA, hB y Dp con nuestra nomenclatura anterior:
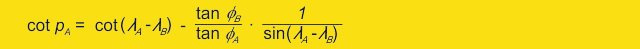
de la ecuación inicial se obtiene también el ángulo en el que se cortó la naranja:

o otra vez a nuestra nomenclatura anterior:

Para el cálculo de la latitud en el círculo máximo usamos de nuevo el mismo conjunto:

como nos gustaría utilizar un valor de longitud específica para p (en lugar de los grados de longitud ya navegados) tenemos que ajustar la posición del recorte de naranja a las coordenadas de los meridianos. Lo hacemos a través de la intersección H:

De esta manera obtenemos la ecuación para la latitud del curso de círculo máximo en función de la longitud:
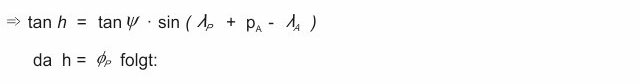


imagen 1
El problema:queremos navegar desde A a B, se conocen las coordenadas (longitud y latitud) de la salida y del destino, lo que queremos saber es:
- la distancia
- el rumbo de brújula al que tenemos que seguir
La distancia puede ser calculada por la siguiente relación, tomada de fuentes pertinentes (Wikipedia)


Si aún convertimos el resultado de grados en minutos de arco (multiplicar por 60) obtenemos la distancia entre A y B en millas náuticas (un minuto de arco en un círculo máximo corresponde por definición a una milla náutica).
Hasta aquí todo bien. Ahora el rumbo. La navegación clásica propone para esto el método del "triángulo de navegación", que es un triángulo esférico llamado "triángulo de polo" que forma un ángulo recto en el vértice (S) entre el curso de círculo máximo y la distancia al Polo Norte (o al Polo Sur):

imagen 2
Con más trigonometría esférica se obtiene el rumbo a la salida y aquel en que se llega al destino, así como puntos de referencia que se requieren para las correcciones del rumbo al seguir el círculo máximo, y por lo tanto para navegar el camino más corto.Después de estar un tiempo ocupado con esto, recordé un método más sencillo de entender para mí. Como un viejo pensador intransigente prefiero orientarme relacionado al ecuador en lugar del Polo Norte (tal vez sólo porque hace más calor allí...) Para esto he utilizado el hecho de que cada círculo máximo se cruza exactamente dos veces con cualquier otro del mismo globo, es decir, a los 2 puntos exactamente opuestos de la esfera (llamémoslos H). Así también lo hace el ecuador con nuestro curso de círculo máximo, de la siguiente manera:

imagen 3
M debe ser el centro de la tierraPara que sea un poco más fácil para los ojos humanos, corté nuestra naranja, pues la corté exactamente la parte donde la línea ecuatorial cruza con nuestro curso de círculo máximo, el resultado es el siguiente:

imagen 4
Ahora queremos determinar la latitud asociada para cualquier longitud p (= longitudes navegados) para obtener puntos de recorrido (P) en nuestro curso para cumplir el círculo máximo. Para hacerlo, primero hay que encontrar la posición y el ángulo del corte de la naranja. Para ello utilizamos la siguiente ecuación: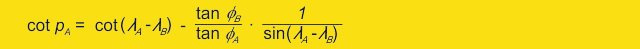
Voy a evitar explicar la derivación de esta ecuación por el momento, las personas interesadas la pueden encontrar más abajo en esta página.
pA nos dice los grados longitudinales que hay que pasar para llegar al bautismo ecuatorial, o hablada como verdulero, el pico de nuestro corte de naranja.
Y con la siguiente ecuación podemos obtener el ángulo en que cortamos la naranja:

(Derivación para los interesados más abajo).
Y ahora, lo que realmente queríamos, una ecuación con la que podemos determinar la latitud correspondiente en el círculo máximo para cualquier longitud dada:

(Derivación como siempre abajo)
Todavía se podía continuar con esto, por ejemplo, sería muy interesante para cada punto de referencia, en qué dirección hay que navegar (el cambio de rumbo de brújula), o determinar la longitud en función de la latitud, o incluso una fórmula para el rumbo sobre tierra, dependiendo de la distancia ya navegada. Con las bases ya desarrolladas se puede derivar todo esto con relativa rapidez con la trigonometría esférica, pero sí que no voy a exagerar aquí...
Lo que nos queda es un
cálculo de prueba:
Acabamos pasar Cabo Horno, y nos gustaría cruzar el Pacífico para llegar a las Islas Fiji. Por supuesto que no haríamos esto normalmente, pero como ejemplo de cálculo funciona agradable :-)
Cabo Horno:
55 grados 59 min S = -55,98 grados
67 grados 17 min W = -67,28 grados
Islas Fiji:
18 grados 8 min S = -18,13 grados
178 grados 26 min O = 178,43 grados
Primero se determina la distáncia para navegar:


= -0,8288 x -0,3112 + 0,5595 x 0,9504 x -0,4114
= -0,0400
arc cos -0,0400 = 87,71 grados (x 60)
= 5.262 millas nauticas
Ahora determinamos el pA requerido:
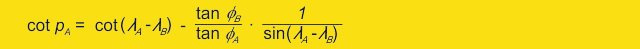
= -0,4513 - 0,2210 x 1,0971
= -0,6938
pA = -55,25 grados
así como el ángulo como cortamos la naranja:

= -0,6750 x -0,8216
= 0,5545
el ángulo de corte de la naranja es entonces 61 grados.
Que pA es negativo significa simplemente, que todavía no hemos llegado al cenit de nuestro círculo máximo durante nuestro viaje, por lo que este valor se refleja a la intersección que tenemos detrás (H' en lugar de H), respectivamente, el ángulo hasta allí.
Ahora queremos determinar cinco puntos en el curso, uno a la salida, otro a la llegada, y tres más en el medio. Nuestra fórmula:

Nuestros longitudes predeterminadas son: -67,28 grados (Cabo Horno, salida); 178,43 grados (Islas Fiji, destino); y también -95 grados; -125 grados; -150 grados. También calculamos el inicio y el destino, aunque ya se conoce las latitudes, sólo para comprobar la exactitud del cálculo.
= 1,8034 x -0,8216 = -1,4817 -> latitud = -55,98 grados, ok para Cabo Horno
= 1,8034 x -0,1815 = -0,3274 -> latitud = -18,13 grados, ok para Islas Fiji
y los 3 puntos de referencia:
= 1,8034 x -0,9925 = -1,7899 -> latitud = -60,81 grados
= 1,8034 x -0,9207 = -1,6604 -> latitud = -58,94 grados
= 1,8034 x -0,6695 = -1,2074 -> latitud = -50,36 grados
Se ve que nuestro curso de círculo máximo nos lleva desde el Cabo Horno inicialmente hacia el sur, hasta 61 grados de latitud (= ángulo de corte de la naranja), probablemente tenemos que luchar duro con hielo allí, antes de que nos dirigimos hacia el norte y se calentará hacia el ecuador...
John Franklin, Amerigo Vespucci y Sir Francis Drake dejan saludar, que no te olvides llevar tu sextante en tu viaje por favor, porque todos eran grandes matemáticos y aún navegando sin GPS...
"Hay algo más importante que la lógica: La imaginación", Alfred Hitchcock
Derivaciones:
Consideramos el triángulo esférico entre el ecuador, nuestro curso de círculo máximo, y un punto arbitrario P (ver imagen 5). Este triángulo tiene excelentes propiedades, es de hecho un triángulo esférico con ángulo recto, y permite por lo tanto fácilmente muchos cálculos. Estamos interesados en la ubicación exacta del corte de la naranja, donde nuestro curso cruza el ecuador, y el ángulo en el que cortamos la naranja. Conocidas son 2 lugares P, es decir, el punto de inicio y del destino, cada uno con latitud y longitud. En este triángulo utilizamos un teorema de la trigonometría esférica:

ahora reemplazamos hA, hB y Dp con nuestra nomenclatura anterior:
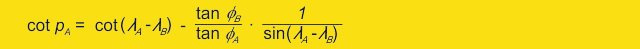
de la ecuación inicial se obtiene también el ángulo en el que se cortó la naranja:

o otra vez a nuestra nomenclatura anterior:

Para el cálculo de la latitud en el círculo máximo usamos de nuevo el mismo conjunto:

como nos gustaría utilizar un valor de longitud específica para p (en lugar de los grados de longitud ya navegados) tenemos que ajustar la posición del recorte de naranja a las coordenadas de los meridianos. Lo hacemos a través de la intersección H:

De esta manera obtenemos la ecuación para la latitud del curso de círculo máximo en función de la longitud:
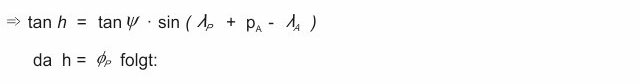

0 comentarios | deja un comentario
más fotos de "Navegación de círculo máximo en la ortodrómica de naranja":
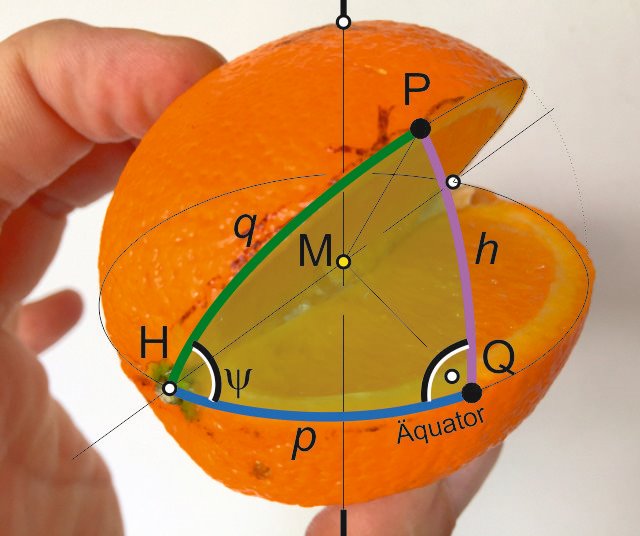
imagen 5

regata en Croacia

y los ganadores fueron...

categorías: Deporte
palabras clave: Navegación, círculo, máximo, ortodrómica, naranja
publicado: 21.04.2016
videos
apartamentos
coches de alquiler
últimos posts:
Nuevos Las Piteras Patio apartamentos
Hace 25 años
Los últimos requisitos para viajar a España
Tengan cuidado al reservar vuelos
Descuentos de verano en Las Piteras
Felices vacaciones de Pascua
Las Piteras en Charco del Palo
La obligación de llevar mascarillas al aire libre ya no es aplicable
Hace 25 años
Los últimos requisitos para viajar a España
Tengan cuidado al reservar vuelos
Descuentos de verano en Las Piteras
Felices vacaciones de Pascua
Las Piteras en Charco del Palo
La obligación de llevar mascarillas al aire libre ya no es aplicable
Otra vez
Feliz año nuevo 2022
Mascarilla nuevamente obligatoria en España a partir de Nochebuena
Navidad 2021
Arquitectura eclesiástica de Lanzarote
Reserve su coche de alquiler lo antes posible
Erupción del volcán Cumbre Vieja en La Palma
Por fin sin mascarilla
Feliz año nuevo 2022
Mascarilla nuevamente obligatoria en España a partir de Nochebuena
Navidad 2021
Arquitectura eclesiástica de Lanzarote
Reserve su coche de alquiler lo antes posible
Erupción del volcán Cumbre Vieja en La Palma
Por fin sin mascarilla
categorías:
ApartamentosCharco del Palo
Sitio web
Playa
Excursiones
Animales
Tiempo
Natación
Eventos
Restaurantes
Música
Deporte
Vela
Corona virus




