GroĂźkreisnavigation auf Orthodrom und Apfelsine


Wenn Sie schon mal von London oder Hamburg nach Los Angeles geflogen sind, ist Ihnen vielleicht aufgefallen, dass Sie zunächst fast nach Nordwesten fliegen, um schließlich in Kalifornien mit südwestlichem Kurs anzukommen. Der kürzeste Weg zwischen 2 Orten auf der Erdkugel folgt keinen Kompasskurs, dem der Kapitän die ganze Strecke über folgen könnte. Das wussten bereits die alten Seefahrer, der Kompasskurs muss permanent geändert werden. Dies nennt man Großkreisnavigation, da man dabei auf einem Großkreis (Orthodrom) um die Welt fährt.
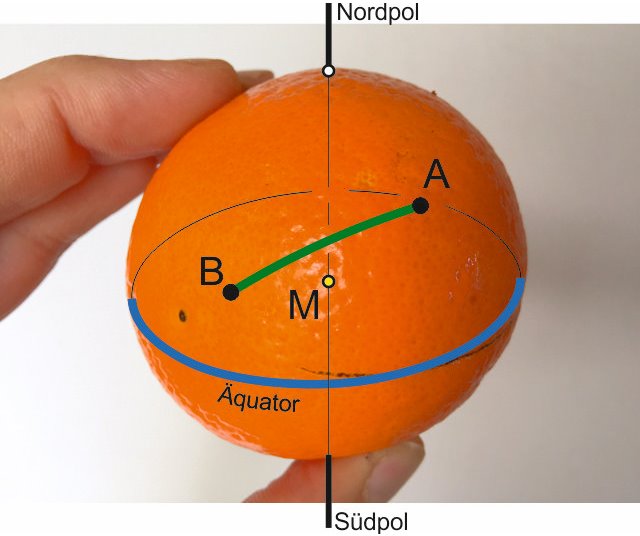
wir wollen von A nach B segeln, die Koordinaten (Längengrade und Breitengrade) von Start- und Zielort sind bekannt, was wir wissen wollen ist:
- die Entfernung
- der Kurs, den wir segeln mĂĽssen
Die Entfernung berechnet sich durch folgenden Zusammenhang aus einschlägigen Quellen (Wikipedia)


Wenn man jetzt noch das Ergebnis von Grad in Bogenminuten umrechnet (also mit 60 multipliziert), so erhält man die Distanz zwischen A und B in Seemeilen (eine Bogenminute auf dem Großkreis entspricht per Definition einer Seemeile).
Soweit so gut. Jetzt noch der Kurs. Die klassische Navigation schlägt dabei die Methode des “Navigationsdreiecks” vor, also ein sphärisches rechtwinliges “Poldreieck”, welches am Scheitelpunkt (S) einen rechten Winkel zwischen Kurs auf dem Großkreis und der Strecke zum Nordpol (oder Südpol) bildet:
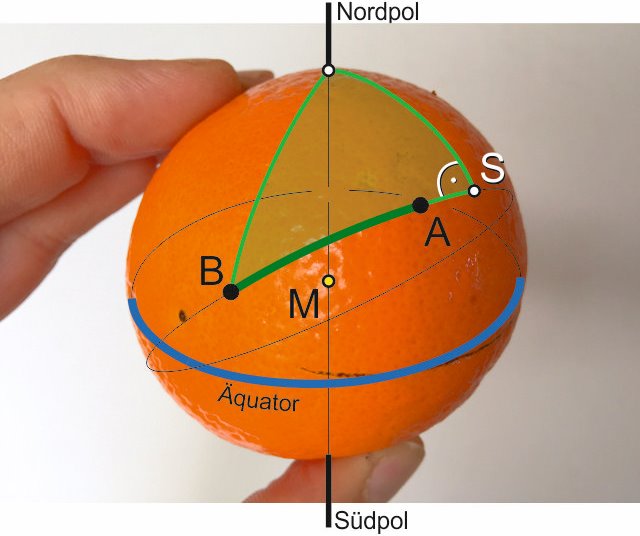
Nachdem ich mich eine Weile damit beschäftigt hatte, fiel mir dann eine für mich einfacher zu verstehende Methode ein. Als alter Querdenker orientiere ich mich lieber am Äquator als am Nordpol (vielleicht aber auch nur, weil es dort wärmer ist...) Dabei nutze ich die Tatsache, dass sich jeder Großkreis mit jedem anderen Goßkreis der selben Kugel genau 2 mal schneidet, und zwar an 2 genau gegenüberliegenden Punkten der Kugel (nennen wie Sie H). Also tut das auch der Äquator mit unserem Kurs - Großkreis, wie folgt:
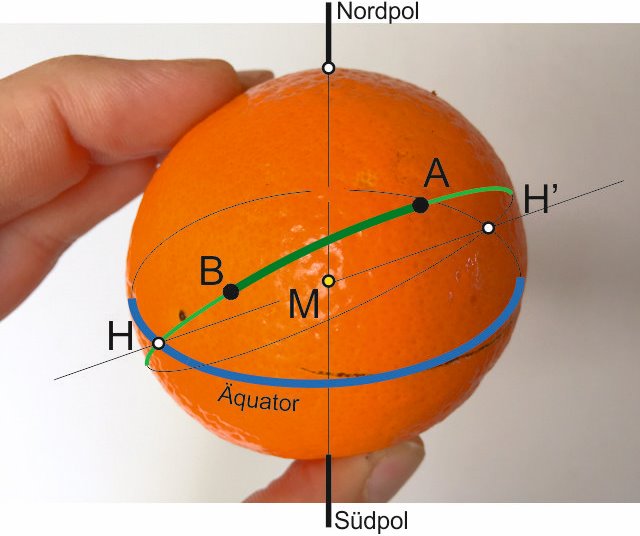
Um es dem Auge etwas einfacher zu machen, habe ich mal aus unserer Orange genau den Teil herausgeschnitten, wo sich der Ă„quator mit unserem Kurs - GroĂźkreis schneidet, das Ergebnis ist folgendes:
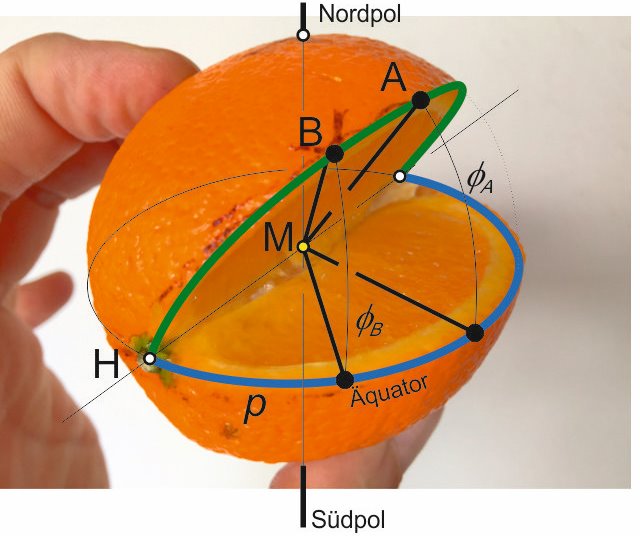
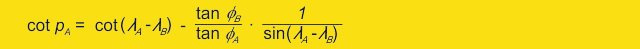
Die Herleitung für diese Gleichung möchte ich Ihnen an dieser Stelle ersparen, Interessierte finden Sie weiter unten auf dieser Seite.
pA liefert als Ergebnis die zu versegelnden Längengrade bis zur Äquatortaufe, oder als Obst- und Gemüsehändler gesprochen, bis zur Spitze unseres Apfelsinenschnitzes.
Mit der folgenden Gleichung erhalten wir den Winkel des Apfelsinenschnitzes:

(Herleitung fĂĽr Interessierte wieder weiter unten.)
Und nun, was wir eigentlich wollen, eine Gleichung, mit der man für jede vorgegebene geografische Länge die zugehörige Breite auf dem Grosskreis ermitteln kann:

(Herleitung wie immer unten)
Man kann das jetzt noch weiter treiben, zum Beispiel wäre es sehr interessant an dem jeweiligen Wegpunkt auch zu wissen, in welche Richtung man weitersegeln soll (Änderung des Kurses über Grund), oder man könnte den Längengrad in Abhängigkeit vom Breitengrad ermitteln, oder auch eine Formel für den erforderlich Kurs über Grund in Abhängigkeit der bereits zurückgelegten Strecke. Mit den bereits erarbeiteten Grundlagen kann man das alles relativ schnell über die sphärische Trigonometrie herleiten, aber ich möchte ja hier nicht übertreiben...
Was uns noch bleibt ist ein
Rechenbeispiel:
Wir haben gerade eben Kap Horn gerundet, und möchten den Pazifik überqueren, um auf den Fidschi Inseln anzukommen. Das würde man normalerweise ja nicht machen, aber als Rechenbeispiel eignet es sich gut :-)
Kap Horn:
55 Grad 59 min S = -55,98 Grad
67 Grad 17 min W = -67,28 Grad
Fidschi Inseln:
18 Grad 8 min S = -18,13 Grad
178 Grad 26 min O = 178,43 Grad
Zunächst ermitteln wir, wie weit wir segeln müssen:


= -0,8288 x -0,3112 + 0,5595 x 0,9504 x -0,4114
= -0,0400
arc cos -0,0400 = 87,71 Grad (x 60)
= 5.262 Seemeilen
Nun ermitteln wir das erforderliche pA:
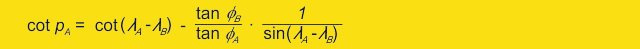
= -0,4513 - 0,2210 x 1,0971
= -0,6938
pA = -55,25 Grad
sowie den Apfelsinenschnitzwinkel:

= -0,6750 x -0,8216
= 0,5545
der Apfelsinenschnitzwinkel ist somit 61 Grad.
Dass pA negativ ist, bedeutet einfach, dass wir auf unserer Segelreise den polnächsten Punkt (Scheitelpunkt des Großkreises) noch nicht erreicht haben, deswegen reflektiert dieser Wert den Schnittpunkt der hinter uns liegt (H' anstelle H) bzw. den Winkel dorthin.
Damit wollen wir nun fĂĽnf Orte auf dem GroĂźkreis - Kurs bestimmen, jeweils einen bei Start- und Zielort, sowie drei dazwischen, dazu unsere Formel:

Unsere vorgegebenen Längengrade sind: -67,28 Grad (Kap Horn, Startort); 178,43 Grad (Fidschi, Zielort); sowie -95 Grad; -125 Grad; -150 Grad. Den Start- und den Zielort beziehen wir einfach mal mit ein, obwohl die Breitengrade ja schon bekannt sind, einfach um die Richtigkeit der Berechnung zu überprüfen.
= 1,8034 x -0,8216 = -1,4817 -> Breite = -55,98 Grad, ok fĂĽr Kap Horn
= 1,8034 x -0,1815 = -0,3274 -> Breite = -18,13 Grad, ok fĂĽr Fidschi
und die 3 Wegpunkte:
= 1,8034 x -0,9925 = -1,7899 -> Breite = -60,81 Grad
= 1,8034 x -0,9207 = -1,6604 -> Breite = -58,94 Grad
= 1,8034 x -0,6695 = -1,2074 -> Breite = -50,36 Grad
Unser Großkreis führt uns also von Kap Horn zunächst noch südlich bis 61 Grad südlicher Breite (= Apfelsinenschnitzwinkel), wahrscheinlich haben wir schwer mit Packeis zu kämpfen dort, bevor er dann immer nördlicher und wärmer wird Richtung Äquator...
John Franklin, Amerigo Vespucci und Sir Francis Drake lassen grüßen, Sie mögen doch bitte Ihren Sextanten auf der Reise nicht vergessen, denn es waren alles große Mathematiker und waren noch ohne GPS unterwegs...
"Es gibt etwas wichtigeres als Logik: Die Vorstellungskraft", Alfred Hitchcock
Herleitungen:
Wir betrachten das sphärische Dreieck zwischen Äquator, unserem Kurs - Großkreis, sowie einem beliebigen Punkt P (siehe Abbildung 5 weiter unten). Dieses Dreieck hat hervorragende Eigenschaften, es ist nämlich ein rechtwinkliges Kugeldreieck und lässt somit ganz einfach Berechnungen zu. Uns interessiert die genaue Lage des Apfelsinenschnitts also wo unser Kurs den Äquator kreuzt, sowie der Winkel, mit dem wir die Orange geschnitten haben. Bekannt sind 2 Orte P, nämlich der Start- und der Zielpunkt der Segeltrips, jeweils mit Längen- und Breitengraden. In diesem Dreieck gilt der Satz aus der sphärischen Trigonometrie:

jetzt ersetzen wir hA, hB und Dp mit unserer bisherigen Nomenklatur:
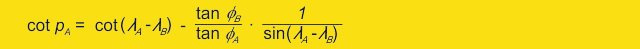
aus der anfänglichen Gleichung erhalten wir auch den Winkel, mit dem die Orange geschnitten wurde:

oder wieder in unserer bisherigen Nomenklatur:

FĂĽr die Berechnung der Breitengrade auf dem Kurs - GroĂźkreis legen wir wieder den selben Satz zugrunde:

da wir aber für p gerne einen konkreten Längengrad einsetzen (anstelle der versegelten Länge) müssen wir die Lage des Orangenschnitzes an die Meridiankoordinaten anpassen. Dies machen wir über den Schnittpunkt H:

somit erhalten wir unsere Gleichung für die Breitengrate auf dem Großkreis - Kurs in Abhängigkeit vom Längengrad:
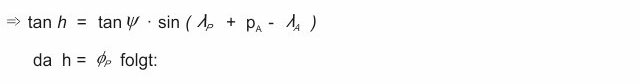


Abbildung 1
Das Problem:wir wollen von A nach B segeln, die Koordinaten (Längengrade und Breitengrade) von Start- und Zielort sind bekannt, was wir wissen wollen ist:
- die Entfernung
- der Kurs, den wir segeln mĂĽssen
Die Entfernung berechnet sich durch folgenden Zusammenhang aus einschlägigen Quellen (Wikipedia)


Wenn man jetzt noch das Ergebnis von Grad in Bogenminuten umrechnet (also mit 60 multipliziert), so erhält man die Distanz zwischen A und B in Seemeilen (eine Bogenminute auf dem Großkreis entspricht per Definition einer Seemeile).
Soweit so gut. Jetzt noch der Kurs. Die klassische Navigation schlägt dabei die Methode des “Navigationsdreiecks” vor, also ein sphärisches rechtwinliges “Poldreieck”, welches am Scheitelpunkt (S) einen rechten Winkel zwischen Kurs auf dem Großkreis und der Strecke zum Nordpol (oder Südpol) bildet:

Abbildung 2
Über sphärische Trigonometrie gelangt man dann auf den Startkurs sowie den Kurs, mit dem man am Zielort ankommt, sowie zu einzelnen Wegpunkten, die man ja für die Kurskorrekturen auf dem Großkreis benötigt, um die kürzeste Strecke zu segeln.Nachdem ich mich eine Weile damit beschäftigt hatte, fiel mir dann eine für mich einfacher zu verstehende Methode ein. Als alter Querdenker orientiere ich mich lieber am Äquator als am Nordpol (vielleicht aber auch nur, weil es dort wärmer ist...) Dabei nutze ich die Tatsache, dass sich jeder Großkreis mit jedem anderen Goßkreis der selben Kugel genau 2 mal schneidet, und zwar an 2 genau gegenüberliegenden Punkten der Kugel (nennen wie Sie H). Also tut das auch der Äquator mit unserem Kurs - Großkreis, wie folgt:

Abbildung 3
M sei dabei stets der Erdmittelpunkt.Um es dem Auge etwas einfacher zu machen, habe ich mal aus unserer Orange genau den Teil herausgeschnitten, wo sich der Ă„quator mit unserem Kurs - GroĂźkreis schneidet, das Ergebnis ist folgendes:

Abbildung 4
jetzt möchten wir für jede beliebige Länge p (= versegelte Längengrade) die zugehörige geografische Breite ermitteln, um beliebige Wegpunkte P auf unserem Kurs - Großkreis zu erhalten. Dazu müssen wir zunächst die Lage und den Winkel des Apfelsinenschnitzes kennen. Dazu bedienen wir uns der folgenden Gleichung: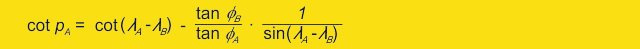
Die Herleitung für diese Gleichung möchte ich Ihnen an dieser Stelle ersparen, Interessierte finden Sie weiter unten auf dieser Seite.
pA liefert als Ergebnis die zu versegelnden Längengrade bis zur Äquatortaufe, oder als Obst- und Gemüsehändler gesprochen, bis zur Spitze unseres Apfelsinenschnitzes.
Mit der folgenden Gleichung erhalten wir den Winkel des Apfelsinenschnitzes:

(Herleitung fĂĽr Interessierte wieder weiter unten.)
Und nun, was wir eigentlich wollen, eine Gleichung, mit der man für jede vorgegebene geografische Länge die zugehörige Breite auf dem Grosskreis ermitteln kann:

(Herleitung wie immer unten)
Man kann das jetzt noch weiter treiben, zum Beispiel wäre es sehr interessant an dem jeweiligen Wegpunkt auch zu wissen, in welche Richtung man weitersegeln soll (Änderung des Kurses über Grund), oder man könnte den Längengrad in Abhängigkeit vom Breitengrad ermitteln, oder auch eine Formel für den erforderlich Kurs über Grund in Abhängigkeit der bereits zurückgelegten Strecke. Mit den bereits erarbeiteten Grundlagen kann man das alles relativ schnell über die sphärische Trigonometrie herleiten, aber ich möchte ja hier nicht übertreiben...
Was uns noch bleibt ist ein
Rechenbeispiel:
Wir haben gerade eben Kap Horn gerundet, und möchten den Pazifik überqueren, um auf den Fidschi Inseln anzukommen. Das würde man normalerweise ja nicht machen, aber als Rechenbeispiel eignet es sich gut :-)
Kap Horn:
55 Grad 59 min S = -55,98 Grad
67 Grad 17 min W = -67,28 Grad
Fidschi Inseln:
18 Grad 8 min S = -18,13 Grad
178 Grad 26 min O = 178,43 Grad
Zunächst ermitteln wir, wie weit wir segeln müssen:


= -0,8288 x -0,3112 + 0,5595 x 0,9504 x -0,4114
= -0,0400
arc cos -0,0400 = 87,71 Grad (x 60)
= 5.262 Seemeilen
Nun ermitteln wir das erforderliche pA:
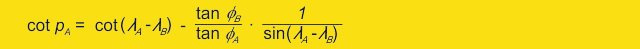
= -0,4513 - 0,2210 x 1,0971
= -0,6938
pA = -55,25 Grad
sowie den Apfelsinenschnitzwinkel:

= -0,6750 x -0,8216
= 0,5545
der Apfelsinenschnitzwinkel ist somit 61 Grad.
Dass pA negativ ist, bedeutet einfach, dass wir auf unserer Segelreise den polnächsten Punkt (Scheitelpunkt des Großkreises) noch nicht erreicht haben, deswegen reflektiert dieser Wert den Schnittpunkt der hinter uns liegt (H' anstelle H) bzw. den Winkel dorthin.
Damit wollen wir nun fĂĽnf Orte auf dem GroĂźkreis - Kurs bestimmen, jeweils einen bei Start- und Zielort, sowie drei dazwischen, dazu unsere Formel:

Unsere vorgegebenen Längengrade sind: -67,28 Grad (Kap Horn, Startort); 178,43 Grad (Fidschi, Zielort); sowie -95 Grad; -125 Grad; -150 Grad. Den Start- und den Zielort beziehen wir einfach mal mit ein, obwohl die Breitengrade ja schon bekannt sind, einfach um die Richtigkeit der Berechnung zu überprüfen.
= 1,8034 x -0,8216 = -1,4817 -> Breite = -55,98 Grad, ok fĂĽr Kap Horn
= 1,8034 x -0,1815 = -0,3274 -> Breite = -18,13 Grad, ok fĂĽr Fidschi
und die 3 Wegpunkte:
= 1,8034 x -0,9925 = -1,7899 -> Breite = -60,81 Grad
= 1,8034 x -0,9207 = -1,6604 -> Breite = -58,94 Grad
= 1,8034 x -0,6695 = -1,2074 -> Breite = -50,36 Grad
Unser Großkreis führt uns also von Kap Horn zunächst noch südlich bis 61 Grad südlicher Breite (= Apfelsinenschnitzwinkel), wahrscheinlich haben wir schwer mit Packeis zu kämpfen dort, bevor er dann immer nördlicher und wärmer wird Richtung Äquator...
John Franklin, Amerigo Vespucci und Sir Francis Drake lassen grüßen, Sie mögen doch bitte Ihren Sextanten auf der Reise nicht vergessen, denn es waren alles große Mathematiker und waren noch ohne GPS unterwegs...
"Es gibt etwas wichtigeres als Logik: Die Vorstellungskraft", Alfred Hitchcock
Herleitungen:
Wir betrachten das sphärische Dreieck zwischen Äquator, unserem Kurs - Großkreis, sowie einem beliebigen Punkt P (siehe Abbildung 5 weiter unten). Dieses Dreieck hat hervorragende Eigenschaften, es ist nämlich ein rechtwinkliges Kugeldreieck und lässt somit ganz einfach Berechnungen zu. Uns interessiert die genaue Lage des Apfelsinenschnitts also wo unser Kurs den Äquator kreuzt, sowie der Winkel, mit dem wir die Orange geschnitten haben. Bekannt sind 2 Orte P, nämlich der Start- und der Zielpunkt der Segeltrips, jeweils mit Längen- und Breitengraden. In diesem Dreieck gilt der Satz aus der sphärischen Trigonometrie:

jetzt ersetzen wir hA, hB und Dp mit unserer bisherigen Nomenklatur:
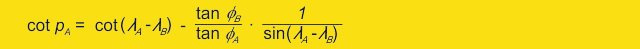
aus der anfänglichen Gleichung erhalten wir auch den Winkel, mit dem die Orange geschnitten wurde:

oder wieder in unserer bisherigen Nomenklatur:

FĂĽr die Berechnung der Breitengrade auf dem Kurs - GroĂźkreis legen wir wieder den selben Satz zugrunde:

da wir aber für p gerne einen konkreten Längengrad einsetzen (anstelle der versegelten Länge) müssen wir die Lage des Orangenschnitzes an die Meridiankoordinaten anpassen. Dies machen wir über den Schnittpunkt H:

somit erhalten wir unsere Gleichung für die Breitengrate auf dem Großkreis - Kurs in Abhängigkeit vom Längengrad:
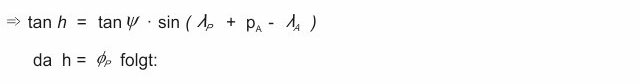

0 Kommentare | Kommentar schreiben
weitere Fotos von "GroĂźkreisnavigation auf Orthodrom und Apfelsine":
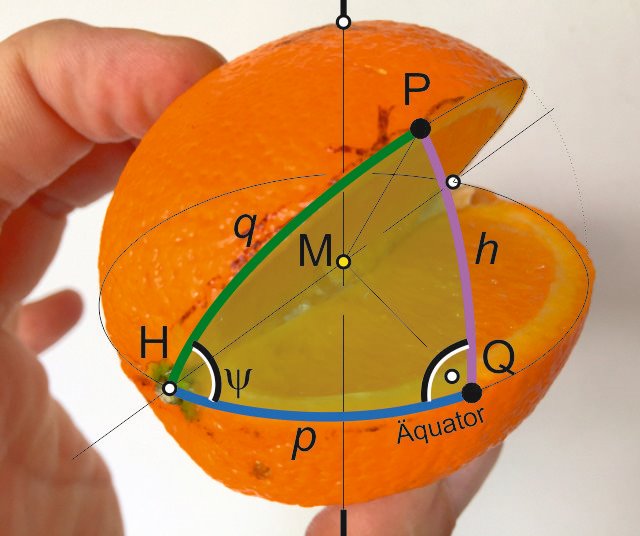
Abbildung 5

Regatta in Kroatien

und die Sieger waren...

Kategorien: Sport
Keywords: GroĂźkreisnavigation, Orthodrom, Apfelsine
gepostet: 21.04.2016
Videos
Apartments
Mietwagen
letzte Posts:
Neue Las Piteras Patio Apartments
Vor 25 Jahren
Die neuesten Reisebestimmungen fĂĽr Spanien
Vorsicht bei Flugbuchungen
Sommer Rabatte in Las Piteras
Schöne Osterfeiertage
Las Piteras in Charco del Palo
Maskenpflicht im Freien entfällt wieder
Vor 25 Jahren
Die neuesten Reisebestimmungen fĂĽr Spanien
Vorsicht bei Flugbuchungen
Sommer Rabatte in Las Piteras
Schöne Osterfeiertage
Las Piteras in Charco del Palo
Maskenpflicht im Freien entfällt wieder
Es ist mal wieder soweit
Alles Gute fĂĽr das Neue Jahr 2022
Erneute Maskenpflicht in Spanien ab Heilig Abend
Weihnachten 2021
Kirchenarchitektur auf Lanzarote
KĂĽmmern Sie sich rechtzeitig um Ihren Mietwagen
Ausbruch des Cumbre Vieja Vulkans auf La Palma
Endlich wieder ohne Maske
Alles Gute fĂĽr das Neue Jahr 2022
Erneute Maskenpflicht in Spanien ab Heilig Abend
Weihnachten 2021
Kirchenarchitektur auf Lanzarote
KĂĽmmern Sie sich rechtzeitig um Ihren Mietwagen
Ausbruch des Cumbre Vieja Vulkans auf La Palma
Endlich wieder ohne Maske
Kategorien:
ApartmentsCharco del Palo
Website
Strand
Ausflüge
Tiere
Wetter
Schwimmen
Veranstaltungen
Restaurants
Musik
Sport
Segeln
Coronavirus




