Great-circle orthodromic navigation on an orange


If you have been flying from London or Hamburg to Los Angeles, you may have noticed that at the beginning you fly almost to northwest, to finally arrive in California with south-westerly course. The shortest distance between 2 places on the globe does't follow a straight compass heading which the captain could follow all the way. This already knew the old sailors, the compass heading needs to be changed permanently. This is called great-circle navigation, since you travel on an orthodromic course around the world.
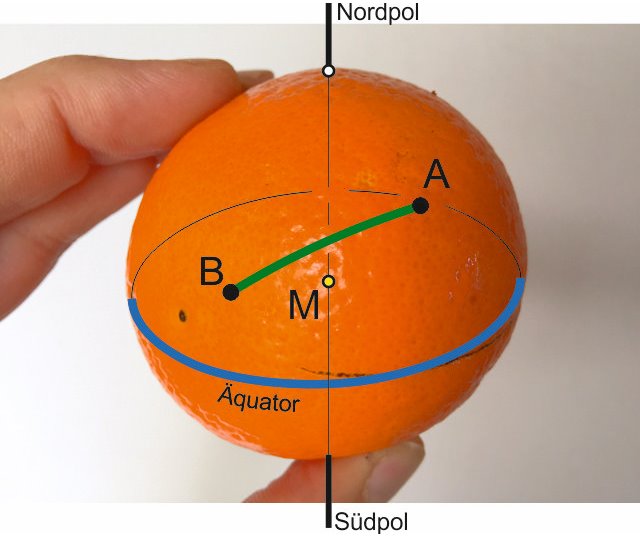
we want to sail from A to B, the coordinates (longitude and latitude) of departure and destination are known, what we want to know is:
- the distance
- the compass heading we have to follow
The Distance can be calculated by the following relationship, taken from relevant sources (Wikipedia)


If we now convert the result from degrees in arcminutes (multiplied by 60) we obtain the distance between A and B in nautical miles (one arcminute on a great-circle corresponds by definition to one nautical mile).
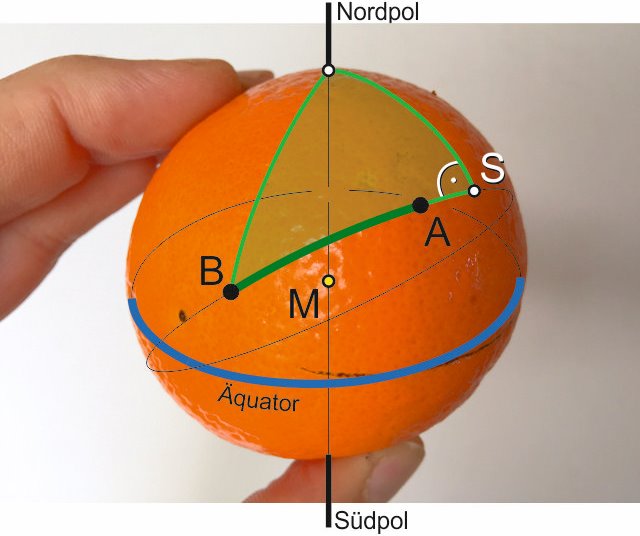
So far so good. Now the heading. The classical navigation proposes the method of the "navigation triangle" which is a spherical right angled "pole-triangle" and forms a right angle at the apex (S) between the great-circle course and the distance to the North Pole (or South Pole):
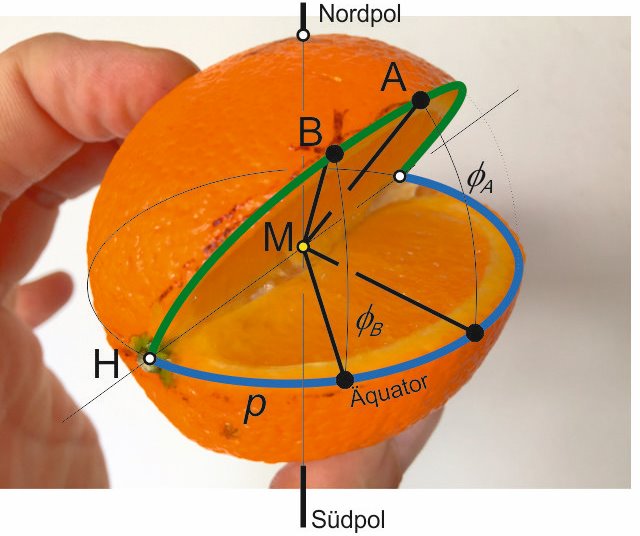
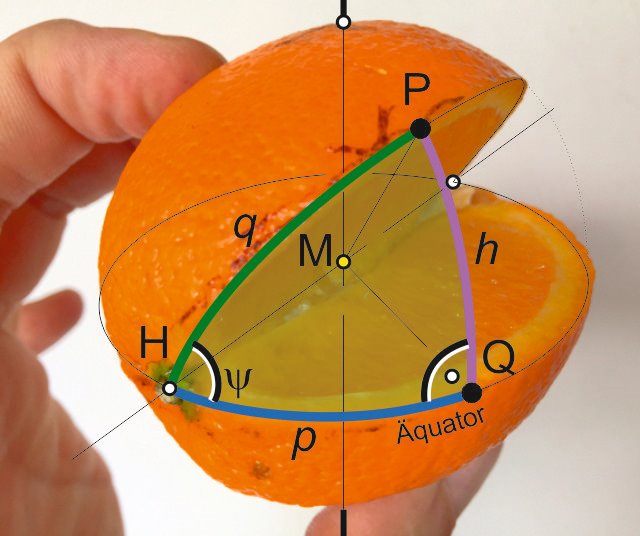
After I was a while busy with this I remembered a more simple method for me to understand. As an old intransigent thinker I prefer to orient myself equator-related rather than at the North Pole (maybe just because it's warmer there...) Here I use the fact that every great-circle intersects exactly twice with each other great-circle on the same globe, namely at 2 exactly opposite points of the sphere (let's call them H). So does also the equator with our great-circle course, as follows:

To make it a bit easier for human's eye, I cut our orange, exactly i cut out the part where the equator intersects with our great-circle course, the result is as follows:
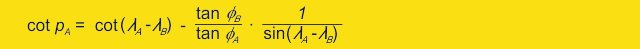
I will avoid to explain the derivation of this equation for the moment, interested people can find it below on this page.
pA tells us as a result the longitudes to be passed to have the equatorial baptism, or spoken as a greengrocer, to the top of our orange carving.
And with the following equation we obtain the angle of the orange carving:

(Derivation for those interested again below.)
And now, what we really wanted, an equation with which one can determine the corresponding lattitude on the great-circle for any given longitud:

(Derivation as always below)
One could still continue with this, for example, it would be very interesting for each waypoint to know in which direction we should sail (changing ground track), or you could determine the longitude as a function of latitude, or even a formula for the required course over ground, depending on the already sailed distance. With the already developed bases one can derive all this relatively quickly with spherical trigonometry, but yes I will not exaggerate here...
What we have pending is a
sample calculation:
We have just rounded Cape Horn, and would like to cross the Pacific to arrive on the Fiji Islands. Of course we would not do this normally, but as a sample calculation it works nice :-)
Cape Horn:
55 degrees 59 min S = -55.98 degrees
67 degrees 17 min W = -67.28 degrees
Fiji Islands:
18 degrees 8 min S = -18.13 degrees
178 degrees 26 min O = 178.43 degrees
First, we determine how far we need to sail:


= -0.8288 x -0.3112 + 0.5595 x 0.9504 x -0.4114
= -0.0400
arc cos -0.0400 = 87.71 degrees (x 60)
= 5,262 nautical miles
Now we define the required pA:
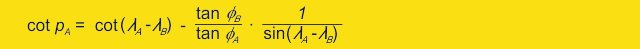
= -0.4513 - 0.2210 x 1.0971
= -0.6938
pA = -55.25 degrees
as well as the orange carving angle:

= -0.6750 x -0.8216
= 0.5545
the orange carving angle is thus 61 degrees.
That pA is negative simply means that we have not yet reached the apex of our great circle during our sailing trip, so this value is reflected to the intersection behind us (H' instead H) respectively the angle to there.
Now We want to determine five places on the great-circle course, each one at start and finish, and three in between. Our formula:

Our predetermined longitudes are: -67.28 degrees (Cape Horn, start); 178.43 degrees (Fiji Islands, destination); as well as -95 degrees; -125 degrees; -150 degrees. We also calculate the start and the destination although the latitudes are already known, just to check the accuracy of the calculation.
= 1.8034 x -0.8216 = -1.4817 -> latitude = -55.98 degrees, ok for Cape Horn
= 1.8034 x -0.1815 = -0.3274 -> latitude = -18.13 degrees, ok for Fiji Islands
and the 3 waypoints:
= 1.8034 x -0.9925 = -1.7899 -> latitude = -60.81 degrees
= 1.8034 x -0.9207 = -1.6604 -> latitude = -58.94 degrees
= 1.8034 x -0.6695 = -1.2074 -> latitude = -50.36 degrees
Our great-circle course thus takes us from Cape Horn initially southwards to 61 degrees latitude (= orange carving angle), probably we have to fight hard with ice there before we will head northwards and it will get warmer towards the equator...
John Franklin, Amerigo Vespucci and Sir Francis Drake are greeting you, that you don´t forget your sextant on the trip please, because they were all great mathematicians and were still sailing without GPS...
"There is something more important than logic: Imagination", Alfred Hitchcock
Derivations:
We consider the spherical triangle between the equator, our great-circle course, and an arbitrary point P (see picture 5 below). This triangle has excellent properties, it is in fact a right-angeled spherical triangle and permits therefore easily calculations. We are interested in the exact location of the orange cutout, where our course crosses the equator, and the angle at which we cut the Orange. Known are 2 places P, namely the start and destination point of sailing trips, each with latitude and longitude. In this triangle we use a theorem of spherical trigonometry:

now we replace hA, hB and Dp with our previous nomenclature:
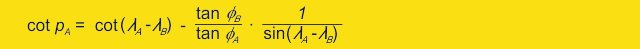
from the initial equation we obtain also the angle at which the orange was cut:

or back to our previous nomenclature:

To calculate the latitude on the great-circle course we use again the same set:

as we like to use a specific longitude value for p (instead of sailed longitud) we have to adjust the position of the orange cutout to meridian coordinates. We do this through the intersection H:

Thus we get our equation for the latitude of the great-circle course depending on the longitude:
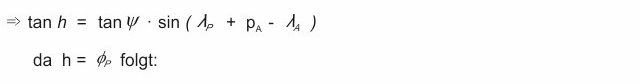


picture 1
The problem:we want to sail from A to B, the coordinates (longitude and latitude) of departure and destination are known, what we want to know is:
- the distance
- the compass heading we have to follow
The Distance can be calculated by the following relationship, taken from relevant sources (Wikipedia)


If we now convert the result from degrees in arcminutes (multiplied by 60) we obtain the distance between A and B in nautical miles (one arcminute on a great-circle corresponds by definition to one nautical mile).
So far so good. Now the heading. The classical navigation proposes the method of the "navigation triangle" which is a spherical right angled "pole-triangle" and forms a right angle at the apex (S) between the great-circle course and the distance to the North Pole (or South Pole):

picture 2
With further spherical trigonometry one gets the heading at departure and the heading at which you arrive at the destination, as well as waypoints which are required for the course corrections to follow the great-circle and so to sail the shortest distance.After I was a while busy with this I remembered a more simple method for me to understand. As an old intransigent thinker I prefer to orient myself equator-related rather than at the North Pole (maybe just because it's warmer there...) Here I use the fact that every great-circle intersects exactly twice with each other great-circle on the same globe, namely at 2 exactly opposite points of the sphere (let's call them H). So does also the equator with our great-circle course, as follows:

picture 3
M hereby should be the center of the earthTo make it a bit easier for human's eye, I cut our orange, exactly i cut out the part where the equator intersects with our great-circle course, the result is as follows:

picture 4
now we want to determine for any length p (= sailed longitudes) the associated latitude to get waypoints (P) on our course - to fulfil a great-circle. To do this we first should find the position and the angle of the orange carving. For this we use the following equation: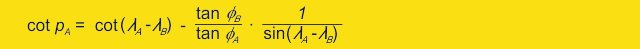
I will avoid to explain the derivation of this equation for the moment, interested people can find it below on this page.
pA tells us as a result the longitudes to be passed to have the equatorial baptism, or spoken as a greengrocer, to the top of our orange carving.
And with the following equation we obtain the angle of the orange carving:

(Derivation for those interested again below.)
And now, what we really wanted, an equation with which one can determine the corresponding lattitude on the great-circle for any given longitud:

(Derivation as always below)
One could still continue with this, for example, it would be very interesting for each waypoint to know in which direction we should sail (changing ground track), or you could determine the longitude as a function of latitude, or even a formula for the required course over ground, depending on the already sailed distance. With the already developed bases one can derive all this relatively quickly with spherical trigonometry, but yes I will not exaggerate here...
What we have pending is a
sample calculation:
We have just rounded Cape Horn, and would like to cross the Pacific to arrive on the Fiji Islands. Of course we would not do this normally, but as a sample calculation it works nice :-)
Cape Horn:
55 degrees 59 min S = -55.98 degrees
67 degrees 17 min W = -67.28 degrees
Fiji Islands:
18 degrees 8 min S = -18.13 degrees
178 degrees 26 min O = 178.43 degrees
First, we determine how far we need to sail:


= -0.8288 x -0.3112 + 0.5595 x 0.9504 x -0.4114
= -0.0400
arc cos -0.0400 = 87.71 degrees (x 60)
= 5,262 nautical miles
Now we define the required pA:
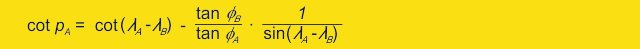
= -0.4513 - 0.2210 x 1.0971
= -0.6938
pA = -55.25 degrees
as well as the orange carving angle:

= -0.6750 x -0.8216
= 0.5545
the orange carving angle is thus 61 degrees.
That pA is negative simply means that we have not yet reached the apex of our great circle during our sailing trip, so this value is reflected to the intersection behind us (H' instead H) respectively the angle to there.
Now We want to determine five places on the great-circle course, each one at start and finish, and three in between. Our formula:

Our predetermined longitudes are: -67.28 degrees (Cape Horn, start); 178.43 degrees (Fiji Islands, destination); as well as -95 degrees; -125 degrees; -150 degrees. We also calculate the start and the destination although the latitudes are already known, just to check the accuracy of the calculation.
= 1.8034 x -0.8216 = -1.4817 -> latitude = -55.98 degrees, ok for Cape Horn
= 1.8034 x -0.1815 = -0.3274 -> latitude = -18.13 degrees, ok for Fiji Islands
and the 3 waypoints:
= 1.8034 x -0.9925 = -1.7899 -> latitude = -60.81 degrees
= 1.8034 x -0.9207 = -1.6604 -> latitude = -58.94 degrees
= 1.8034 x -0.6695 = -1.2074 -> latitude = -50.36 degrees
Our great-circle course thus takes us from Cape Horn initially southwards to 61 degrees latitude (= orange carving angle), probably we have to fight hard with ice there before we will head northwards and it will get warmer towards the equator...
John Franklin, Amerigo Vespucci and Sir Francis Drake are greeting you, that you don´t forget your sextant on the trip please, because they were all great mathematicians and were still sailing without GPS...
"There is something more important than logic: Imagination", Alfred Hitchcock
Derivations:
We consider the spherical triangle between the equator, our great-circle course, and an arbitrary point P (see picture 5 below). This triangle has excellent properties, it is in fact a right-angeled spherical triangle and permits therefore easily calculations. We are interested in the exact location of the orange cutout, where our course crosses the equator, and the angle at which we cut the Orange. Known are 2 places P, namely the start and destination point of sailing trips, each with latitude and longitude. In this triangle we use a theorem of spherical trigonometry:

now we replace hA, hB and Dp with our previous nomenclature:
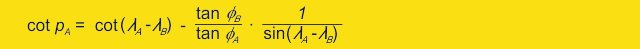
from the initial equation we obtain also the angle at which the orange was cut:

or back to our previous nomenclature:

To calculate the latitude on the great-circle course we use again the same set:

as we like to use a specific longitude value for p (instead of sailed longitud) we have to adjust the position of the orange cutout to meridian coordinates. We do this through the intersection H:

Thus we get our equation for the latitude of the great-circle course depending on the longitude:
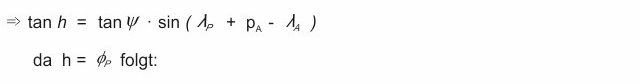

0 comments | leave a comment
more photos from "Great-circle orthodromic navigation on an orange":
picture 5

regatta in Croatia

and the winners were...

categories: Sports
keywords: Great-circle, orthodromic, navigation, orange
posted: 21.04.2016
videos
apartments
rent a car
last postings:
New Las Piteras Patio apartments
25 years ago
The latest travel regulations for Spain
Be careful when booking flights
Summer discounts in Las Piteras
Happy Easter holidays
Las Piteras in Charco del Palo
Mask requirement outdoors is no longer applicable
25 years ago
The latest travel regulations for Spain
Be careful when booking flights
Summer discounts in Las Piteras
Happy Easter holidays
Las Piteras in Charco del Palo
Mask requirement outdoors is no longer applicable
Again and again
Happy New Year 2022
Mask again mandatory in Spain from Christmas Eve
Christmas 2021
Church architecture on Lanzarote
Reserve your hired car as soon as possible
Eruption of the Cumbre Vieja volcano on La Palma
Finally without mask
Happy New Year 2022
Mask again mandatory in Spain from Christmas Eve
Christmas 2021
Church architecture on Lanzarote
Reserve your hired car as soon as possible
Eruption of the Cumbre Vieja volcano on La Palma
Finally without mask
categories:
ApartmentsCharco del Palo
Website
Beach
Excursions
Animals
Weather
Swimming
Events
Restaurants
Music
Sports
Sailing
Corona virus




